COVID-19_1.html

Last week, we introduced an article on "Infection Simulation" as a homework assignment for students during spring break.

I have been playing with programming since yesterday. Instead of improving the "Go-Game model" (Ohtsuka,1971) I wrote a processing code from scratch using the algorithm in the above article. Now that I have it running, I would like to show here a few examples. The high infection rate example in the article could not be realized with the parameters in the article, and the values are slightly different. Similarly, I tried to create an example similar to the medium and low infectivity examples in the article, but the parameters are quite different. It may be that my calculation logic and the design of the infection contact part are different. However, the infectivity of the moving programming screen in the example in this article is quite high, so I think it cannot be realized with α=0.1, but it may be a bug in my program.

For those who are interested, I have prepared my prototype below, so please try it yourself. Please note that you need to install the original Processing language.

I am running it on Linux, but it should also work on Windows and Mac. Simply copy and paste the following program into the Processing window and press the Run button (right-facing triangle). Graphs can be created in Excel or calc from the csv file that is exported at the same time. Experiment with various parameters. Note that I am a former BASIC programmer, so I am not familiar with variables. I am a former BASIC programmer, so I am not very good with variables, etc.

4/14 addition. There is a point by an information science expert that the relationship between simulation of infectious diseases and the "Goishi Model" essentially depends on the problem of percolation (the "Goishi Model" is said to be essentially equivalent to percolation).

For Thai students and teachers, here is my COVID-19 infection simulation running on Processing. The algorithm is from the following site,
https://rad-it21.com/サイエンス/michikoshi-shugo_20200331/
Sorry, this site provides only in Japanese.
You can download my program from my web site,
http://yossi-okamoto.net/programs/Corona_Sim_ST3.pde
(new version including void effect, parameter VP is as follows)
http://yossi-okamoto.net/programs/COVID_19_ST.pde
Also you need to install Processing platform from here,
https://processing.org/
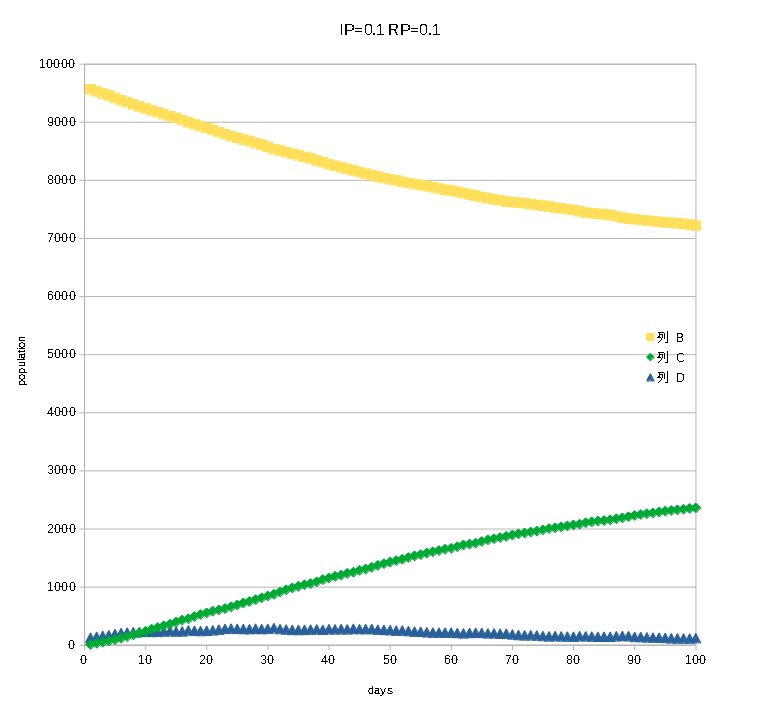
You can run this program under your any choice of parameters. Particularly, IP (infection probability) and RP (recovery probability) are important to study the behavior of infection process. This is a typical cell automaton and can make easily general epidemic curves from its .csv files using Excel or Calc. Please see the images in the previous Japanese version. If you have any questions, please let me know!

100ステップ後のグラフ．人数は100×100の格子で計算．しかし周期境界条件は入れていない．従って端のデータを含んでいないので，初期人数は10000人よりも少ない．青色が感染者．黄色が非感染者，緑が快復者（免疫獲得者）．単位時間を仮に１日とすると100日分の計算になる．記事では確率をどちらも0.1に設定しているが，私の計算ではアルゴリズムが異なるので，その記事のグラフは実現できない．

Graph plot after 100 steps(100days). The number of people is calculated on a 100 x 100 grid. However, periodic boundary conditions are not included. Therefore, the initial number is less than 10000 because the end data are not included. Blue: infected persons. Yellow are the non-infected (white circles above chart), and green are those who have recovered (acquired immunity). Assuming that the unit time is one day, the calculation is for 100 days. In the reference article, the probability is set to 0.1 for both cases, but the reference paper graph is not reproduced in my calculations. Because of the difference of the basic algorithms.