COVID-19_2.html

巣ごもりプロジェクトその２．感染シミュレーションプロトタイプの改良　 FaceBookに５月に書いた記事を載せます．何かの参考に　　14th July 2020, 3rd Jan. 2021

Stay Home (Nesting) project part 2: Improvement of the infection simulation prototype. I wrote an article about it in May on FaceBook. For your reference 14th July 2020

昨日の感染Simを少し改良して，人間の配置に隙間があるとどうなるかを計算しました．密接を避ける効果が明らかになります．新たなパラメータVPが隙間の割合を示します．VPが0.25ということは，隙間が全体の格子の25%あるということです．

なお今回のSimが以前にご紹介した「碁石モデル」の改良版との違いは，碁石モデルでは，感染（地震における破壊）するかどうかのサイコロを振るときに，感染しない場合は即，免疫が生じたとしていたのですが，今回は感染しない場合は放置です．また免疫は感染した格子のみが，ある一定時間経って確率RPで回復し免疫を生じるという風に変えています．
さらに感染確率IPの意味は単位時間（ここでは１日と考えてもよい）で何人に感染させるかという確率です．IPが0.25ということは，４人の人に隣合うとき，うち１人を平均して感染させるという意味です．また感染は格子が隣あうときにのみ生じて，それ以外の遠い人には及びません．これをコンタクトプロセスと呼ぶようです．またRPは快復して免疫を生じる確率ですが，例えばこれが0.05ということは，一度感染した人は平均20日程度で快復して免疫を生じるということです．今回の空隙パラメータを追加したプログラムはこれです．（4/17追記．グラフの人数は空隙率を無視していることに気付きました．実際には格子全体から空隙を引いたものが全体の人数になります）
http://yossi-okamoto.net/programs/COVID_19_ST.pde

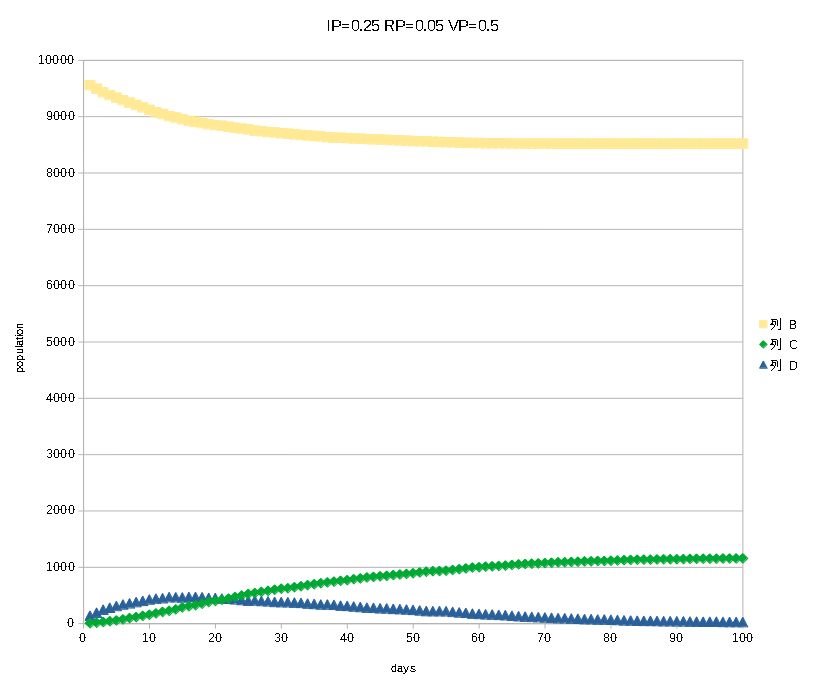
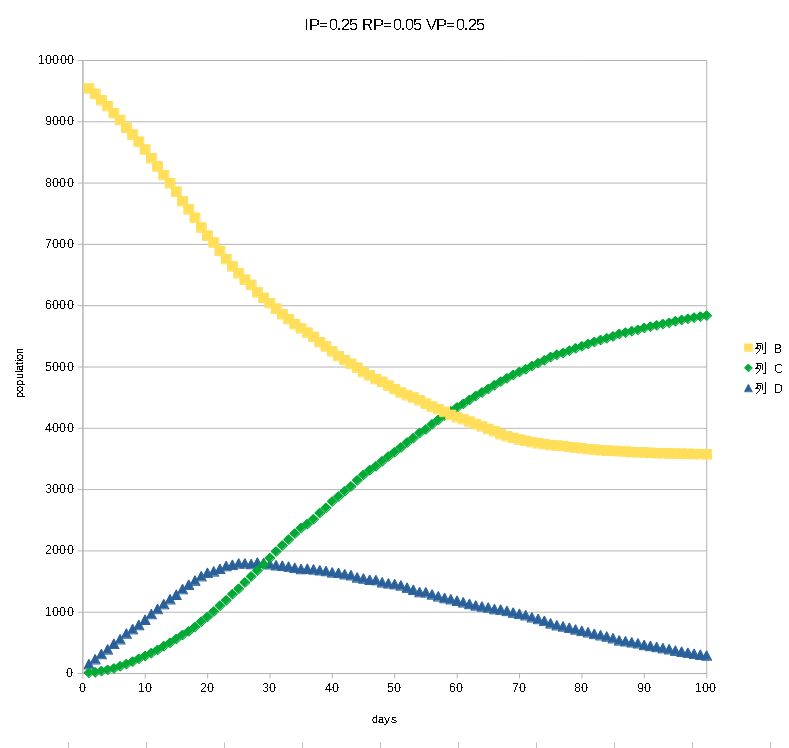
I improved yesterday's infection sim a little and calculated what happens if there are gaps among human grids. The effect of avoiding closeness becomes clear. A new parameter VP indicates the percentage of occupying gaps: VP of 0.25 means that there are 25% of gaps in the whole lattice.

The difference between 1) this simulation and 2) the improved version of the "Goishi Model(Go-Game Model, Ohtsuka,1971)" introduced previously is the treatment of immune. In the case of 1) the original Goishi Model, when the dice decides the lattice is infected (destroyed in an earthquake), nothing happens. However if it is not infected, the lattice is considered immune immediately (means the site is rigid, so no destruction happens after that). In the new model, however, 2) the case of no infection site is left alone, and only the infected lattice is immune to infection after a certain period of time, with a probability of recovery (RP).

The probability of infection IP is the probability of infecting a given number of people in a unit of time (in this case, one day). 0.25 IP means that when 4 people are next to each other, one of them will be infected on average. In addition, infection occurs only when the lattices are adjacent to each other, and not to other distant persons. This is called "contact process". The RP is the probability of recovery and immunity. 0.05, for example, means that once infected, a person will recover and become immune in about 20 days on average. This is the program to which the void parameter was added. (Added on 4/17. I noticed that the number of people in the graph ignores the porosity. In reality, the total number of people is the total lattice minus the voids.)

http://yossi-okamoto.net/programs/COVID_19_ST.pde

白が未感染者，灰黒が空いた格子（空隙），青が感染者，黄色が快復して免疫を獲得した格子．紫が初期感染者を表します．以前の計算と同様にIP=0.25，RP=0.05で間隙率VP=0.25で計算しています．時間ステップで20ステップ目（20日経過）を示しています．わずかな空隙があることで，急速な感染の拡大が避けられているのがわかります．なお，格子は100×100で初期感染者数は100人をランダムに配置してから，計算をスタートしています．

White circle represents uninfected individuals, gray-black represents empty grids (voids), Blue represents infected individuals, and green represents those who have recovered and acquired immunity. Purple represents initially infected individuals. As in previous calculations, IP=0.25, RP=0.05, and the porosity VP=0.25. The 20th time step (after 20 days) is shown. It can be seen that the rapid spread of infection is avoided by the presence of small gaps (voids). The grid is 100 x 100 and the initial number of infected persons is 100 randomly placed before starting the calculations.

時間のグラフにしたところ．未感染者の黄色が下がっているものの，全体人口の４割程度は100日経過後も感染していないことがわかります．青色は感染者数の推移．緑は快復者（免疫を所持）数です．以前の同様の確率計算の図と比べてみてください．

A graph of tim series. Although the number of uninfected persons in yellow is decreasing, about 40% of the total population remains uninfected after 100 days. Blue indicates the number of infected persons. Green is the number of people who have recovered from the disease (i.e., who are immune). Please compare this figure with the previous similar probability calculation.

感染確率などは同じで，空隙率を半分VP=0.5で計算すると，未感染者の減り方がゆるやかになり，100日後でも８割五分の人が感染せずにすんでいることがわかります．単純な計算ではありますが，感染症にとって人の間隔をあけることの重要性が示されています．

The probability of infection is the same, and when the void ratio is higher at half VP = 0.5, the decrease in the number of uninfected persons becomes slower, indicating that 80% of the uninfected persons remain uninfected even after 100 days. Although this is a simple calculation, it shows the importance of spacing between people for infectious diseases.