COVID-19_3.html

Nestling Project Infection Simulation Part 3. I posted the article in May on FaceBook. For your reference 14th July 2020, 17th Apr.2021, revised on 26th Feb. 2024, particularly about colors.

At the bottom of this page, I posted a method for saving a sequence of images and making a movie from them using Processing. This is very useful. It may be helpful for those who have difficulties in saving and creating simulation movies in their research. 17th Apr.2021

3rd Jan. 2021 The color of the graph was changed to match the simulation. (The color of the infected person in Part 1 and 2 was blue, but here it has been changed to red-purple).

エージェントが移動する場合の計算の試作に取り組んでいました．この格子にいる人（複雑系科学ではagentと呼ぶ）をランダムに移動させた場合を考えます．参考記事にも最後にこの計算が載っています．これ先週からアルゴリズムを考えていたのですが，結構大変でした．最初様々な移動のアルゴリズムを考えては計算し，バグが見つかり，また別のアルゴで計算の繰り返しでした．やっと満足のいく試作ができました．まだバグがあるかも知れませんが，少し公開します．感染症の専門家が人が移動して接触することの危険性をさかんに訴えていますが，それが簡単なモデルで実証できます．計算上の100日後の画像とグラフをどうぞ．動画も追加しました．
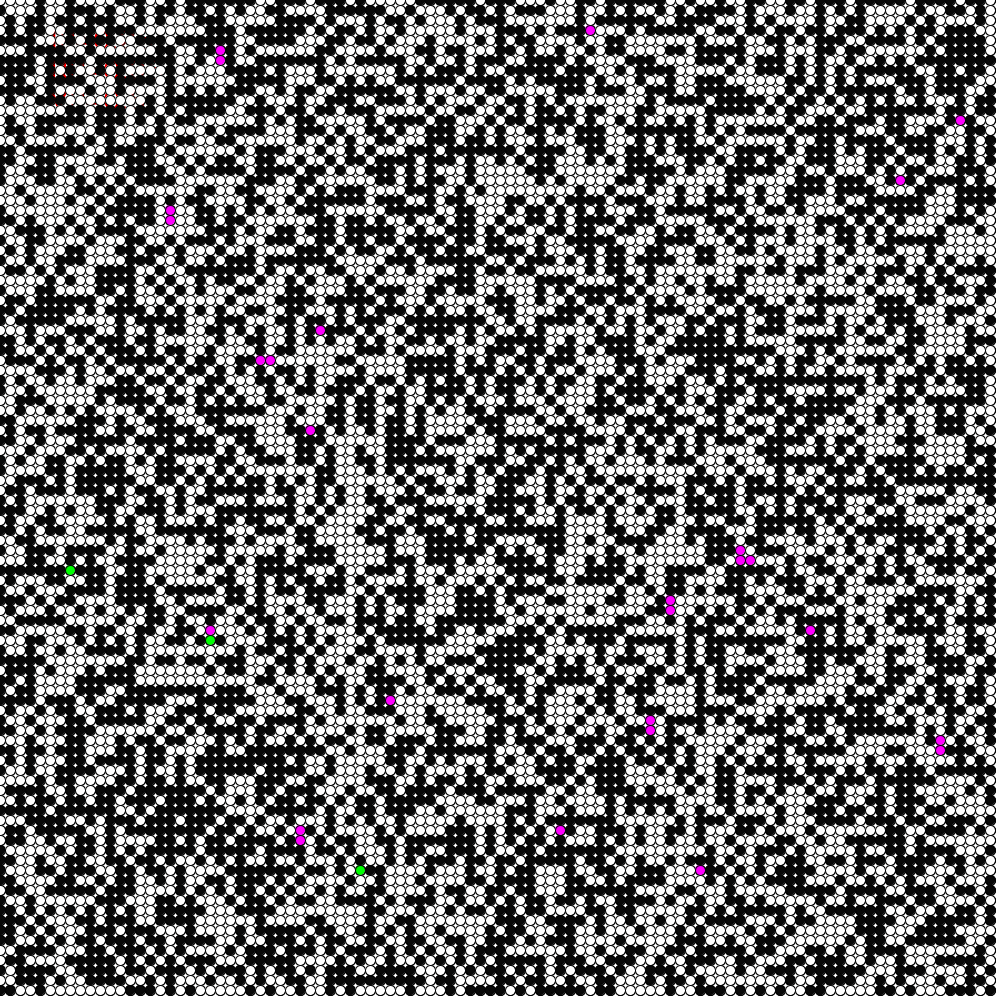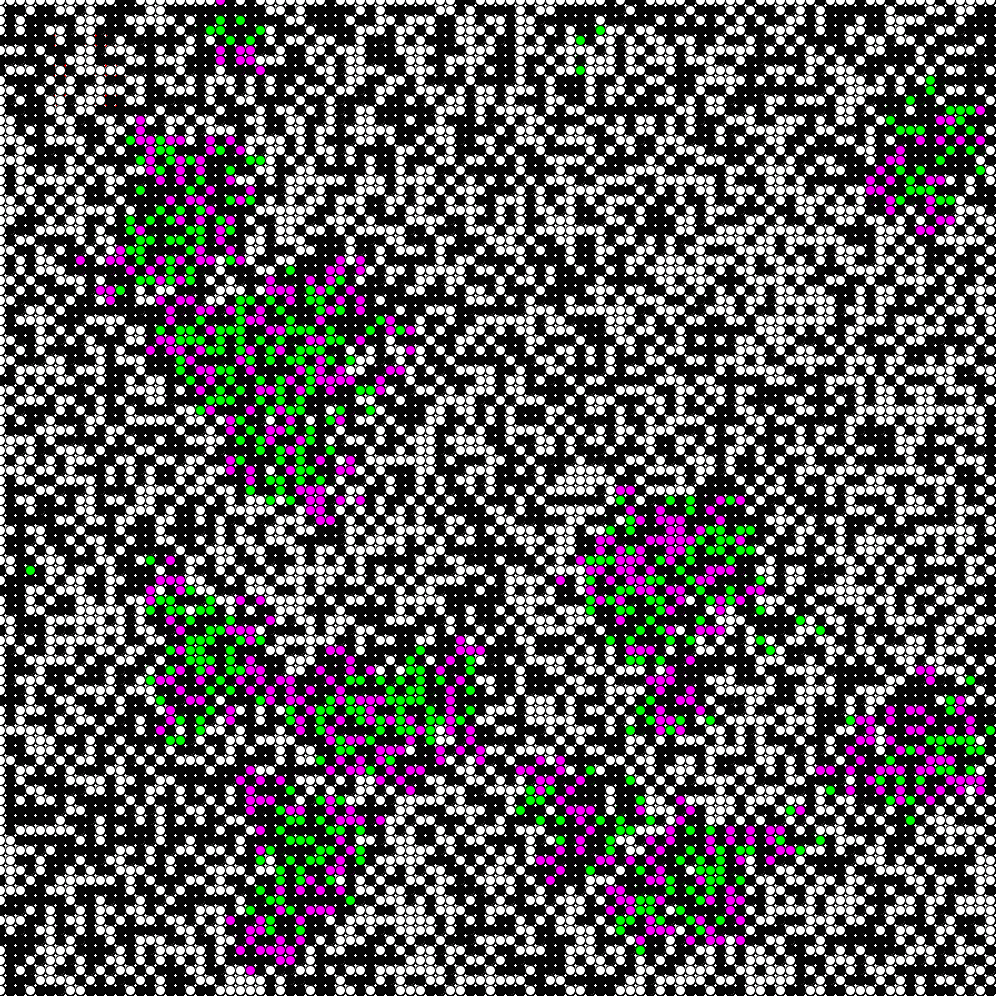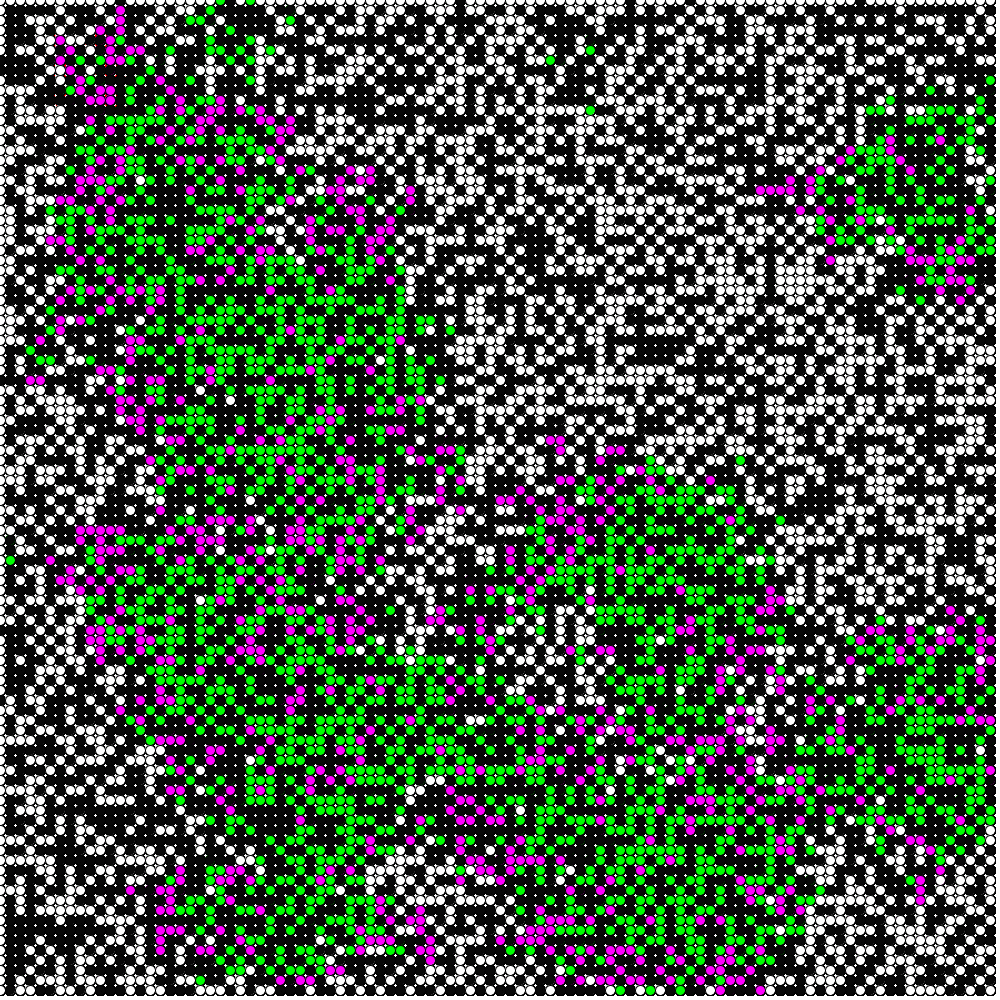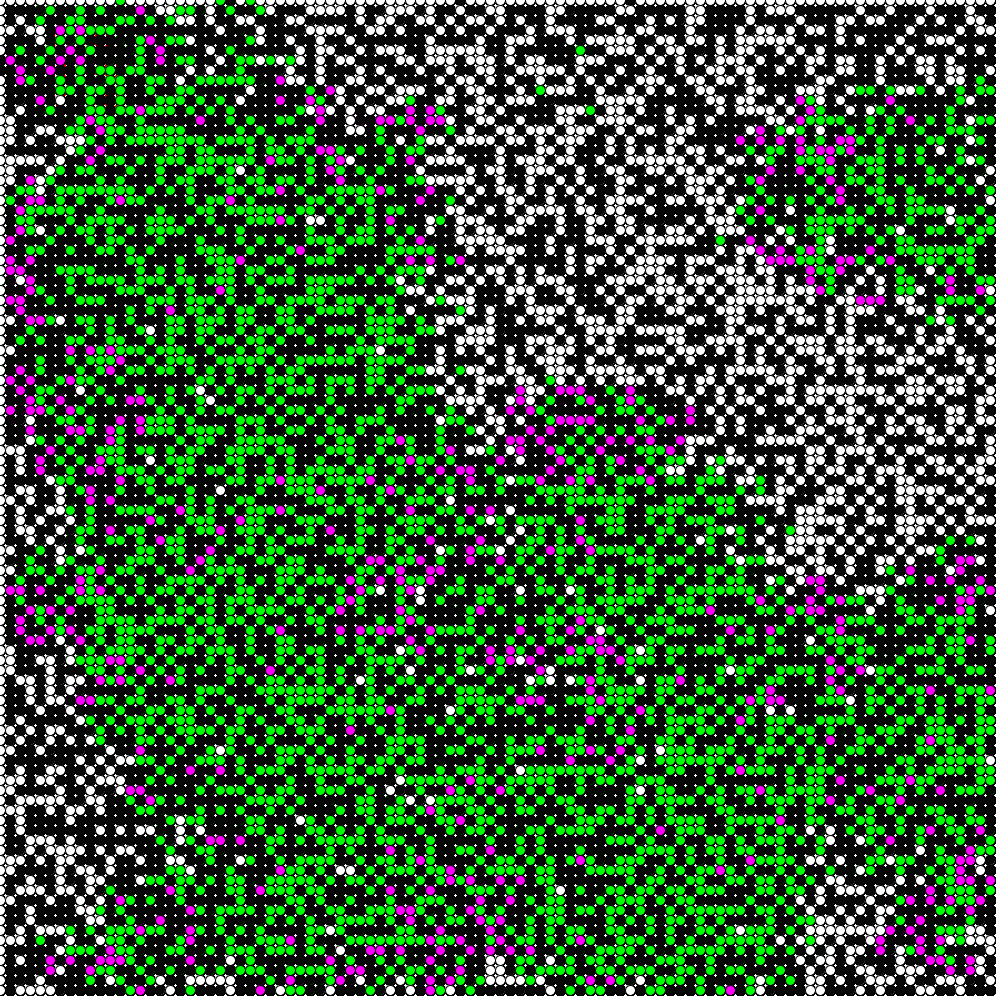
画像では白が非感染者，黒が空隙，紫が現在の感染者．緑が感染後すでに免疫を獲得した人です．移動は格子上の人がある確率MPで移動します．MP=0.25ということは１計算単位（この場合は１日）につき，全体の25%の人がランダムに選ばれて，ランダムな方向（東西南北）に格子１つ分だけ移動します．この確率は格子全体に対する確率です．その他は前の計算と同じ条件です．グラフは黄色のグラフが非感染者数の推移．紫が現在の感染者数の推移．緑が免疫を獲得した人の推移です．（今書いていて，移動確率を人数にせずに，格子全体での確率にしたのはわかりにくいですね．近いうちに改良します．---すみませんまだ修正できていません．2024年2月26日）

I was working on a prototype calculation for the case where the agent moves. Consider the case where a person in this lattice (called an agent in complex systems science) is moved randomly. You can see this calculation at the end of the reference article. I have been working on the algorithm for the last week, and it was quite difficult. At first, I thought of various movement algorithms, calculated them, found a bug, and repeated the calculation with another algorithm. Finally, I was able to create a prototype that I am satisfied with. There may still be some bugs, but I would like to share some of them with the public. Infectious disease experts have often stressed the dangers of people moving and coming into contact with each other, and this can be demonstrated with a simple model. Here are some images and graphs of the calculated 100 days. We have also added a movie.

In the image, white is uninfected, black is a void, and purple is currently infected. Green is the person who has already acquired immunity after infection. The people on the grid move with a certain probability MP, where MP=0.25 means that 25% of the people are randomly selected per unit of calculation (in this case, one day) and move in a random direction (east, west, north, south, south) for one grid position. This is the probability for the entire lattice. Other conditions are the same as in the previous calculation. The yellow graph shows the number of uninfected persons. Purple is the current number of infected persons. The green graph shows the number of immunized persons. (It is difficult to understand why I used the probability of migration for the entire lattice instead of the number of people. I will improve it in the near future.)----Sorry，this has been not fix yet(26th Feb.2024).

感染確率（感染者が１日のうちにほかの人にうつす確率）IP=0.25，快復確率（感染者が１日のうちに快復する確率）RP=0.05，空隙率VP=0.5，移動する確率MP=0.0（移動のない場合）の100日後の計算結果．白が非感染者，黒は空隙，紫が現在の感染者，緑が快復して免疫を得た人．初期の感染者は20名からスタート．格子数は100x100で１万，この計算では空隙率が半分と高いので，人があまり密集していないため，感染は自然に収まってきている．人数は格子の半分の約5000人．初期感染者は20名であるが，クラスターはいくつか重なってきているので，クラスターの数はそれより小さい．

Probability of infection (probability that an infected person will infect others in a day) IP=0.25, probability of recovery (probability that an infected person will recover in a day) RP=0.05, void fraction VP=0.5, and probability of migration MP=0.0 (in the absence of migration) after 100 days. White, non-infected; black, void; purple, currently infected; green, recovered and immunized. The initial number of infected individuals starts at 20. The number of lattices is 100x100, which is 10,000. Since the porosity of the lattice is half of the lattice, the number of infected people is not so dense, and the infection has been naturally controlled. The number of people is about 5,000, half the number on the grid. In this calculation, the porosity is as high as half, so the population is not too dense, and the infection is naturally contained. 20 people are initially infected, but the number of clusters is smaller than that because the clusters overlap.

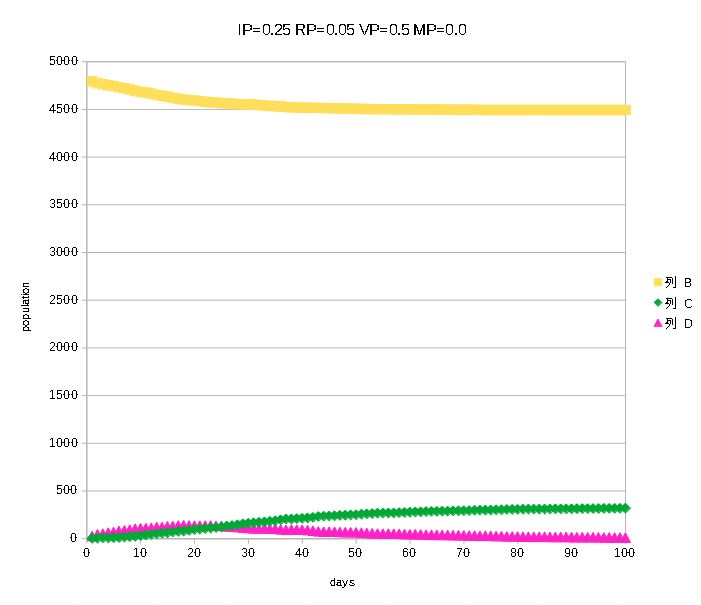
さきほどの条件での，全体の人数から感染者数を引いた非感染者数（黄色），現在の感染者数（紫），快復者数（緑）の時間推移のグラフ．100日分を表示．この計算では非感染者の数は4500名あたりで打ち止め．つまり途中で流行の終焉を迎えていることがわかる．

他の条件は同じで，移動の確率を０からMP=0.05，つまり全体の格子の5%（約50名）が１日ごとにランダムに移動する場合の計算（これ人数に対する％にした方がわかりやすいけれど，ちょっと面倒なので格子全体の％にしている）．わずか５％（人数にすれば10%）の移動で，感染が徐々に進み始めていることがわかる．また現在の感染者（紫色，現在ほかの人に感染させる能力を持った人）も多いことがわかる．

The other conditions are the same, and the probability of migration is calculated from 0 to MP=0.05, i.e., 5% (about 50 persons) of the entire lattice moves randomly every day (it would be easier to understand this as a percentage of the number of persons, but it is a bit cumbersome, so we use a percentage of the entire lattice). It can be seen that the infection is gradually beginning to progress after only 5% (10% of the total number of people) of the total number of people have moved. The number of currently infected persons (purple, those who have the ability to infect others) is also large.

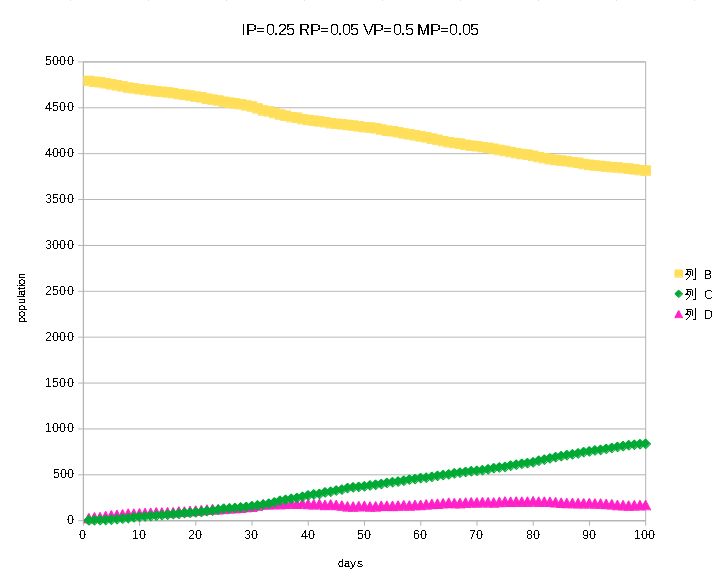
さきほどの全体の格子あたり５％(人口では10%）の移動のグラフ．黄色が以前としてどんどん減り続けている．つまり流行は収まるどころか増え続けていることがわかる．紫色の現在の感染者の数もそれほど減っていない．

さらに移動確率を格子全体の25%，つまり人数の半分が移動するという条件にすると，果てしなく感染が広がりだしているのがわかる．

Furthermore, when the probability of movement is set to 25% of the entire lattice, i.e., half of the number of people move, we can see that the infection is spreading endlessly.

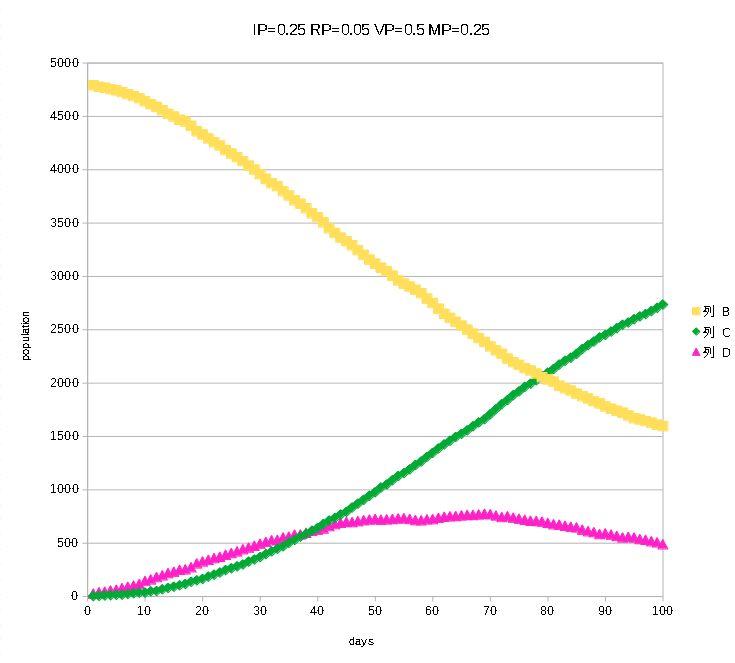
時系列のグラフ．全体の人数の2/3がすでに罹患していることになる．黄色のグラフの減少が最後に少し鈍りだしているのは，格子の空きがなくなり始めていることによると思われる．つまり計算格子をもっと大きくとるとおそらくこの鈍りはなくなる．別の言い方をするとこの閉じられた集団での集団免疫の効果が出はじめているということになる．実際に現在の感染者数（紫色）のグラフは減り始めている．非常に簡単なモデル計算ではあるが，感染症パンデミックに見られる様々な特徴をよく表しているように思える．

Time series graph. Two thirds of the total number of people have already been infected. The decrease in the yellow graph seems to slow down a little at the end, probably due to the fact that the grid is starting to run out of space. In other words, a larger computational grid would probably eliminate this slowdown. In other words, the effect of "herd immunity" in this closed population is beginning. In fact, the graph of the current number of infections (purple) is beginning to decrease. Although this is a very simple model calculation, it seems to represent well the various characteristics of an infectious disease pandemic.

さきほどの最後の条件で，計算経過の動画を作ってみました．Processingのよいところは，繰り返し計算のときにframeごとに画像を保存させることができます．たった１行
saveFrame("frames/######.png");
と書くだけです．これで連番の画像ファイルが作れることに今気付きました．アニメーションを作るには大変おすすめの技法ですよ！ちなみに連番ファイルからGIFアニメを作るには，私はLinux上のImageMagickのconvertコマンドを使っています．たとえばこんな感じ．
convert -delay 30 -loop 0 *.png movie.gif
めちゃ便利です！！
と書いてさらに，調べると何とProcessingはムービーメーカーという機能があって，それで動画を作れるそうです！！知らなかった！
https://office606.org/archives/1267/

I have made a video of the calculation process under the last condition described above.

The nice thing about Processing is that you can save an image for each frame of an iterative calculation. Just one line

saveFrame("frames/######.png");

is all that is needed. I just realized that I can create sequentially numbered image files with this. I highly recommend this technique for creating animations! By the way, I use ImageMagick's convert command on Linux to create GIF animations from sequentially numbered files. For example

convert -delay 30 -loop 0 *.png movie.gif

It is very convenient!

And then I found out that Processing has a function called Movie Maker, with which you can make movies! I didn't know that!
https://office606.org/archives/1267/